Amaç: Verilem bir \(f(x)\) fonksiyonunun n. dereceden türevini hesaplamak.
Amaç2: Verilen bir veri setinden n. dereceden türevi hesaplamak.
Sonlu Farklar Yaklaşıklığı (Finite Difference Approximation)
Taylor serisini hatırlayalım.
\[
\begin{align*}
f(x+h)=& f(x) + f'(x)h + \frac{f''(x)}{2!}h^2 + \frac{f'''(x)}{3!}h^3 + \cdots \\
f(x+2h)=& f(x) + f'(x)2h + \frac{f''(x)}{2!}(2h)^2 + \frac{f'''(x)}{3!}(2h)^3 + \cdots \\
f(x-h)=& f(x) - f'(x)h + \frac{f''(x)}{2!}h^2 - \frac{f'''(x)}{3!}h^3 + \cdots \\
f(x+2h)=& f(x) + f'(x)2h + \frac{f''(x)}{2!}(2h)^2 + \frac{f'''(x)}{3!}(2h)^3 + \cdots
\end{align*}
\]
Denklemlerin sağ ve sol tarafları belirli şekillerde toplayalım.
\[
\begin{align*}
f(x+h) + f(x-h) =& 2f(x) + 2\frac{f''(x)}{2!}h^2 + \cdots \\
f(x+h) - f(x-h) =& 2f'(x)h + 2\frac{f'''(x)}{3!}h^3 + \cdots
\end{align*}
\]
ve
\[
\begin{align*}
f(x+2h) + f(x-2h) =& 2f(x) + 2\frac{f''(x)}{2!}(2h)^2 + \cdots \\
f(x+2h) - f(x-2h) =& 2f'(x)2h + 2\frac{f'''(x)}{3!}(2h)^3 + \cdots
\end{align*}
\]
İlk Merkezi Farklar Yaklaşıklığı (First Central Difference Approximation)
\(f(x+h) - f(x-h)\) ile ilde ettiğimiz denklemden birinci türevi hesaplayabiliriz.
\[
\begin{align*}
f'(x) = \frac{f(x+h) - f(x-h)}{2h} + \mathcal{O}(h^2)
\end{align*}
\]
Burada \(\mathcal{O}(h^2)\) terimi \(h^2\) ’den daha küçük olduğu için ihmal edilebilir.
\[
\begin{align*}
\mathcal{O}(h^2) = - \frac{f'''(x)}{3!}h^3 + \cdots
\end{align*}
\]
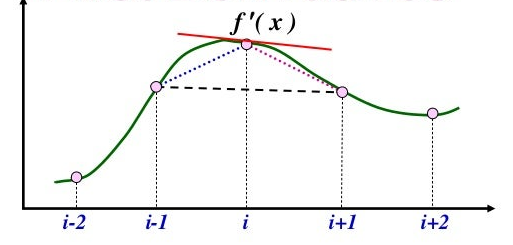
Geometrik yorumu şu şekildedir.
Kaynak : Slideshare
\(x\) noktasında birinci türevi elde ederken \(f\) fonksiyonunun \(x\) ’in bir önceki noktadaki değeri ve bir sonraki noktadaki değeri kullanılır. Bu nedenle merkezi farklar yaklaşıklığı denir. (Merkezi )Fonksiyonların değerlerinin farkına bakıldı. (Farklar )
Birinci dereceden \(h\) bağlılığından sonraki terimleri, yani \(\mathcal{O}(h^2)\) ’yi ihmal ettik. Bu ihmal türev teriminin hassasiyetini belirleyecek. (İlk )
İkinci dereceden türevi hesaplamak için ise \(f(x+h) + f(x-h)\) ile ilde ettiğimiz denklemden yararlanabiliriz.
\[
\begin{align*}
f''(x) = \frac{f(x+h) - 2f(x) + f(x-h)}{h^2} + \mathcal{O}(h^2)
\end{align*}
\]
Üçüncü dereceden türevi aşağıdaki gibi hesaplayabiliriz.
\[
\begin{align*}
f'''(x) = \frac{f(x+2h) - 2f(x+h) + 2f(x-h)-f(x-2h) }{2h^3} + \mathcal{O}(h^2)
\end{align*}
\]
Türev ifadelerini bir tablo haline getirelim.
İlk Merkezi Farklar Yaklaşıklığı
\(2hf'(x)\) -1
0
1
\(h^2f''(x)\) 1
-2
1
\(2h^3f'''(x)\) -1
2
0
-2
1
\(h^4f^{(4)}(x)\) 1
-4
6
-4
1
İlk, Merkezi Olmayan Farklar Yaklaşıklığı (First Non-Central Difference Approximation)
Yukarıdaki tabloya baktığımızda \(f(x)\) fonksiyonunun uç noktalarında türevi hesaplayamadığımızı görebiliriz. Bu nedenle uç noktalarda türevi hesaplayabilmek için başka bir yöntem kullanmalıyız.
\[
\begin{align}
f'(x)= \frac{f(x+h) - f(x-h)}{2h} + \mathcal{O}(h)
\end{align}
\]
Burada \(f(x+h)\) terimi son noktada, \(f(x-h)\) terimi ise ilk noktada hesaplanamaz. Taylor açılımını daha farklı tanımlayalım.
İlk Noktayı Hesaplamak İçin
\[
\begin{align}
f'(x)= \frac{f(x+h) - f(x)}{h} + \mathcal{O}(h)
\end{align}
\]
Son Noktayı Hesaplamak İçin
\[
\begin{align}
f'(x)= \frac{f(x) - f(x-h)}{h} + \mathcal{O}(h)
\end{align}
\]
Böylelikle fonksiyonun her noktasında türev alabildik. Merkezi değerleri kullanmayı bıraktık. (Non-Central )
Tabloyu güncelleyelim.
İlk, Merkezi Olmayan Farklar Yaklaşıklığı , İleri Sonlu Fark
\(hf'(x)\) -1
1
\(h^2f''(x)\) 1
-2
1
\(h^3f'''(x)\) -1
3
-3
1
\(h^4f^{(4)}(x)\) 1
-4
6
-4
1
İlk, Merkezi Olmayan Farklar Yaklaşıklığı , Geri Sonlu Fark
\(hf'(x)\) -1
1
\(h^2f''(x)\) 1
-2
1
\(h^3f'''(x)\) -1
3
-3
1
\(h^4f^{(4)}(x)\) 1
-4
6
-4
1
Daha hassas türev almak için ne yapmalıyız?
İkinci Merkezi Olmayan Sonlu Farklar Yaklaşıklığı (Second Non-Central Finite Difference Approximation)
Taylor serisini biraz daha genişletelim.
\[
\begin{align*}
f(x+h) = f(x) + f'(x)h + \frac{f''(x)}{2!}h^2 + \frac{f'''(x)}{3!}h^3 + \frac{f^{(4)}(x)}{4!}h^4 + \cdots \\
f(x+2h) = f(x) + f'(x)2h + \frac{f''(x)}{2!}(2h)^2 + \frac{f'''(x)}{3!}(2h)^3 + \frac{f^{(4)}(x)}{4!}(2h)^4 + \cdots \\
\end{align*}
\]
Bu iki denklemi aşağıdaki gibi yazalım.
\[
\begin{align*}
f(x+2h) - 4f(x+h) = -3f(x) - 2hf'(x) + \frac{h^{4}}{2} f^{(4)}(x) + \cdots \\
\end{align*}
\]
Birinci dereceden türevi aşağıdaki gibi hesaplayabiliriz.
\[
\begin{align*}
f'(x) = \frac{f(x+h) - f(x)}{h} - \frac{h}{2} f''(x) + \mathcal{O}(h^2)
\end{align*}
\]
İkinci dereceden türevi aşağıdaki gibi hesaplayabiliriz.
\[
\begin{align*}
f''(x) = \frac{f(x+2h) - 2f(x+h) + f(x)}{h^2} + \mathcal{O}(h)
\end{align*}
\]
Şimdi birinci dereceden türev içerisindeki \(f''(x)\) yerine yukarıdaki bulduğumuz terimi koyalım.
\[
\begin{align*}
f'(x)= \frac{f(x+h) - f(x)}{h} - \frac{h}{2} \left( \frac{f(x+2h) - 2f(x+h) + f(x)}{h^2} + \mathcal{O}(h) \right) + \mathcal{O}(h^2) \\
\end{align*}
\]
İkinci dereceden türev terimini kullanarak birinci dereceden türevi hesaplayabiliriz. (İkinci )
\[
\begin{align*}
f'(x)= \frac{-f(x+2h) + 4f(x+h) - 3f(x)}{2h} + \mathcal{O}(h^2)
\end{align*}
\]
İnterpolasyon İle Türev Alma
Veri noktları kullanılarak interpolasyon yapılır ve interpolasyon polinomu elde edilir. Bu polinomun türevi alınır.
Kübik Spline kullanarak türevini almak istediğin noktadaki fonksiyon bulunur ve o fonksiyonun türevi alınır.
Fizikte Kullanılan Türevler
hız
\(v=\frac{dx}{dt}\) Genel
Konum
Hız
Fourier Kanunu
\(q=-k\frac{dT}{dx}\) Sıcaklık İletimi
Sıcaklık
Sıcaklık Akısı
Ohm Kanunu
\(J=-\sigma \frac{dV}{dx}\) Akım Debisi
Volt
Akım Akısı
Newton Viskozite Kanunu
\(\tau=\mu\frac{du}{dx}\) Akışkanlar
Hız
Kesme Gerilimi
Kaynak : Introduction to Engineering and Scientific Computing with Python, David E. Clough, Steven C. Chapra, 1. Baskı, 2022
Bilgisayarda kullanımı
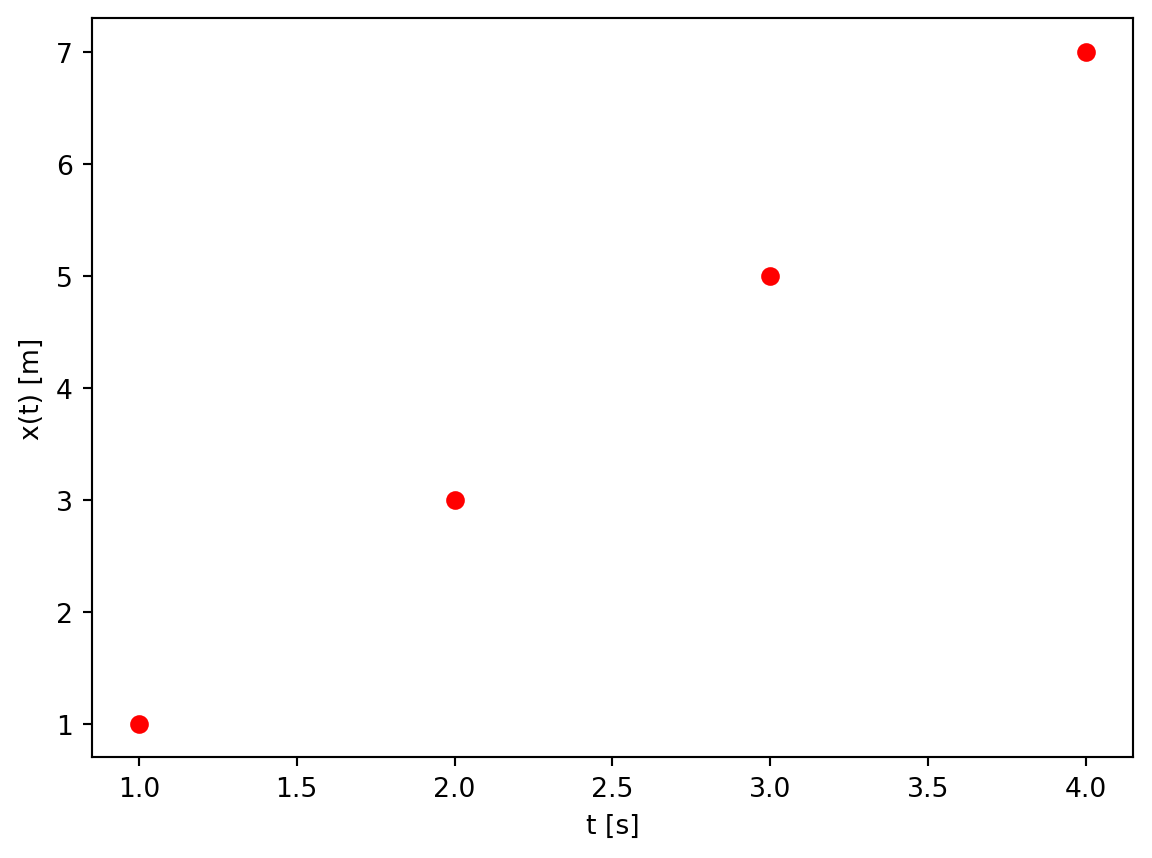
Farz edelim ki bir arabanın konumu belirli saniyelerle ölçülsün.
Bu verileri kullanarak arabanın hızını hesaplayalım.
import numpy as npimport matplotlib.pyplot as plt= np.array([[1 ,1 ],2 ,3 ],3 ,5 ],4 ,7 ]])# Grafiği çizdirelim 0 ],veri[:,1 ],'ro' )'t [s]' )'x(t) [m]' )
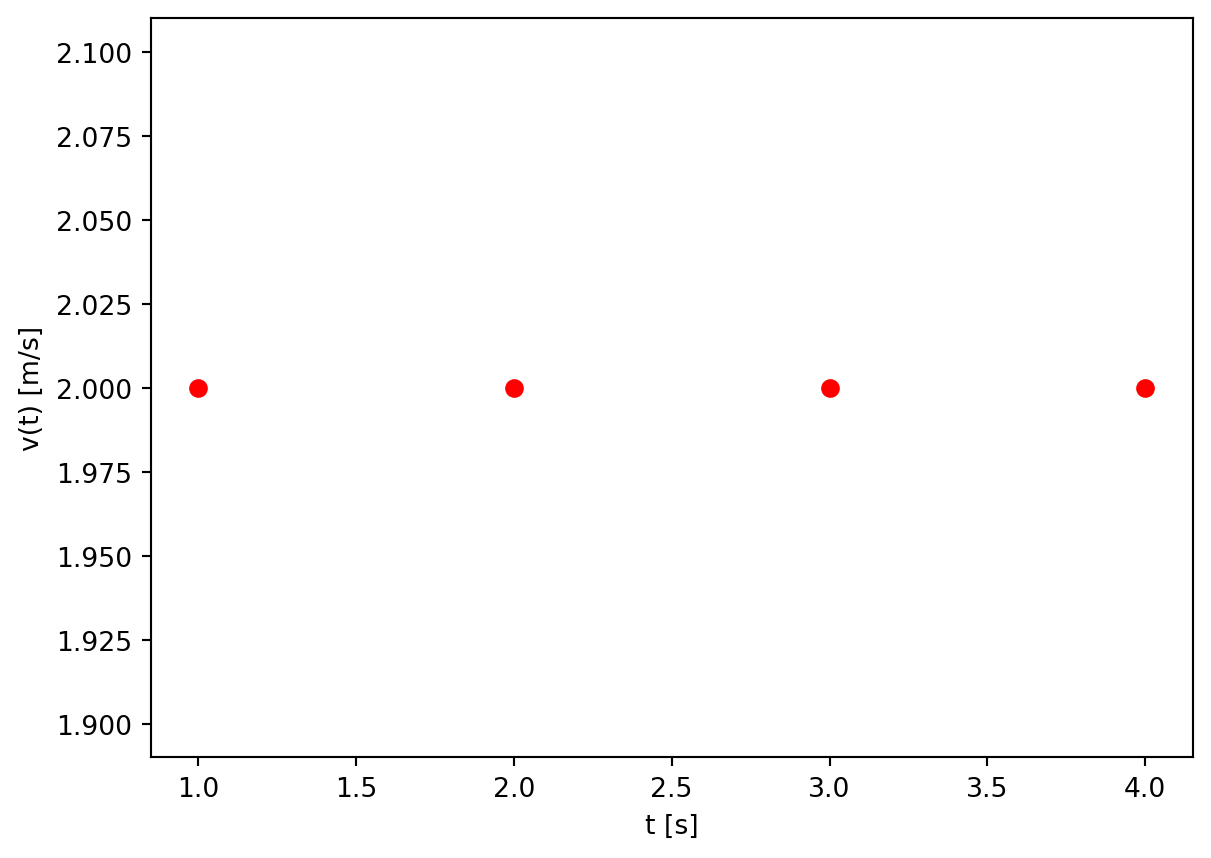
Türev Alma Fonksiyonu
import numpy as npimport matplotlib.pyplot as pltdef turev_merkezi_olmayan_ilk_birinci(veri):= veri[:,0 ]= veri[:,1 ]= len (xVeri)# Turev terimi bir adet eksik olacak. # turev değişkeninin ilk sütunu xVerisi, ikinci sütunu türev değeri olacak. = np.zeros((veriAdeti,2 ))# Adım aralığı sabit ise # h=xVeri[1]-xVeri[0] # Birinci dereceden türev algoritması for i in range (veriAdeti- 1 ):0 ]= xVeri[i]1 ]= (yVeri[i+ 1 ]- yVeri[i])/ (xVeri[i+ 1 ]- xVeri[i])# turev[i,1]=(yVeri[i+1]-yVeri[i])/h # Son terimin türevi - 1 ,0 ]= xVeri[- 1 ]- 1 ,1 ]= (yVeri[- 1 ]- yVeri[- 2 ])/ (xVeri[- 1 ]- xVeri[- 2 ])return turev# Türev Hesapla = turev_merkezi_olmayan_ilk_birinci(veri)= turev[:,0 ]= turev[:,1 ]# Grafiği çizdirelim 'ro' )'t [s]' )'v(t) [m/s]' )
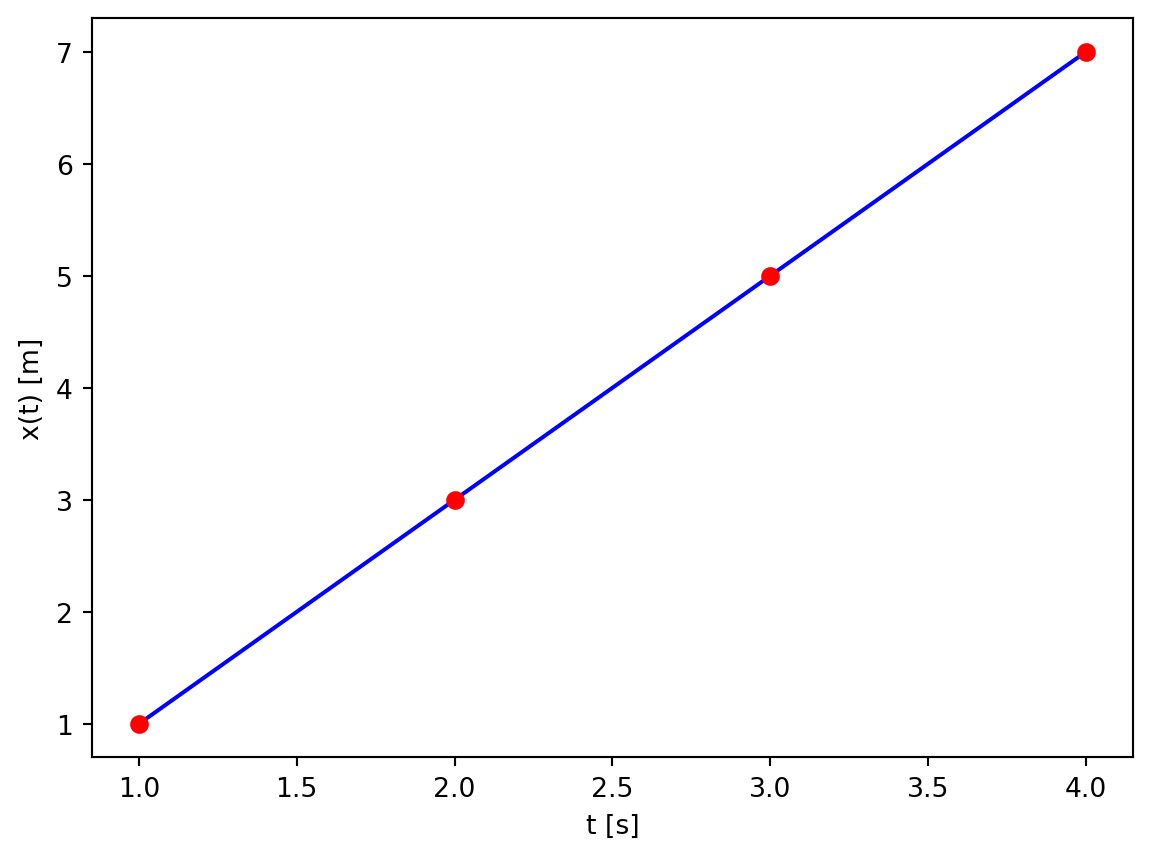
İnterpolasyon
import numpy as npimport matplotlib.pyplot as plt# Veriyi scipy ile interpolasyon yapalım. LAgrange polinomu kullanalım from scipy.interpolate import lagrange= lagrange(veri[:,0 ],veri[:,1 ])# Polinomu çizdirelim = np.linspace(1 ,4 ,100 )'b-' )0 ],veri[:,1 ],'ro' )'t [s]' )'x(t) [m]' )# Polinomu yazdıralım print (polinom)# Polinomun sadece katsayılarını yazdıralım print (polinom.c)# Bu polinomun türevini alalım = polinom.deriv()print (turevPolinom)# Polinomun türevini çizdirelim 'b-' )'ro' )'t [s]' )'v(t) [m/s]' )
3 2
-2.22e-16 x + 8.882e-16 x + 2 x - 1
[-2.22044605e-16 8.88178420e-16 2.00000000e+00 -1.00000000e+00]
2
-6.661e-16 x + 1.776e-15 x + 2